Zadania
Poniżej przedstawiono treść przykładów rozwiązanych w dalszej części strony. Możesz najpierw spróbować je zrobić samodzielnie lub przejść od razu do rozwiązań.
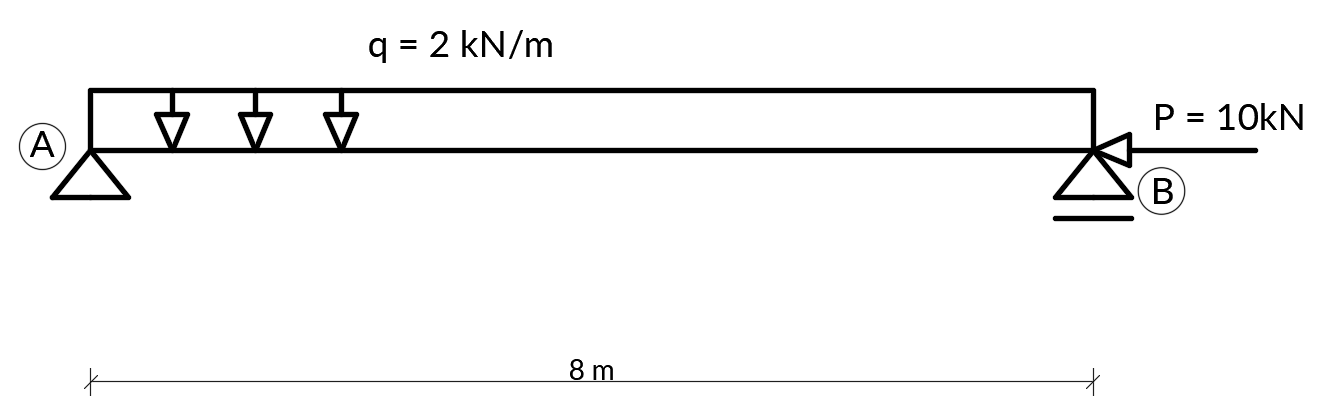
- Znajdź wartości reakcji i narysuj wykresy M, V, N.
- Znajdź wartości reakcji i narysuj wykresy M, V, N.
- Znajdź wartości reakcji i narysuj wykresy M, V, N.
- Znajdź wartości reakcji i narysuj wykresy M, V, N.
- Znajdź wartości reakcji i narysuj wykresy M, V, N.
 Przejdź do rozwiązania
Przejdź do rozwiązania
 Przejdź do rozwiązania
Przejdź do rozwiązania
 Przejdź do rozwiązania
Przejdź do rozwiązania
 Przejdź do rozwiązania
Przejdź do rozwiązania
 Przejdź do rozwiązania
Przejdź do rozwiązania
- Rozwiązanie zadania nr 1
- Rozwiązanie zadania nr 2
- Rozwiązanie zadania nr 3
- Rozwiązanie zadania nr 4
- Rozwiązanie zadania nr 5
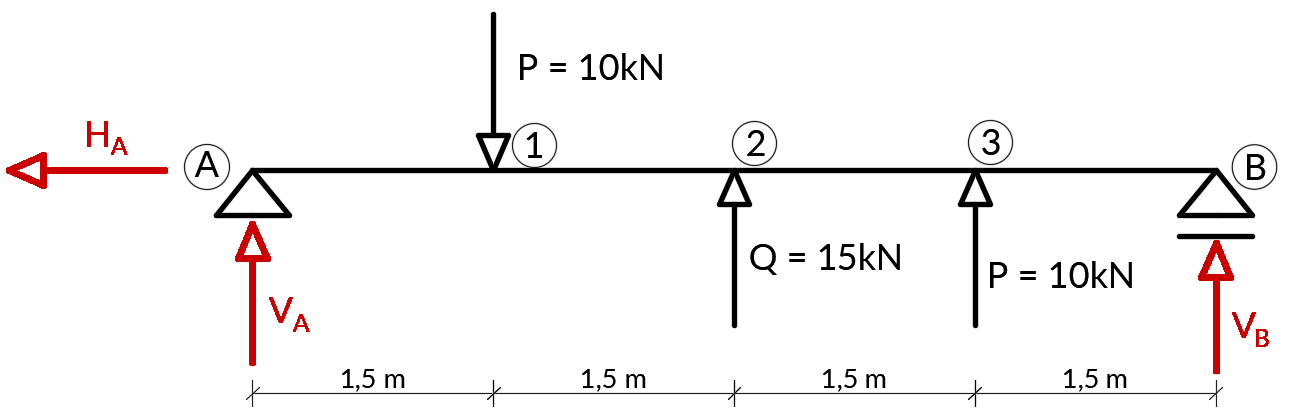
Na rysunku wyżej przyjęto już oznakowania i zwroty reakcji. Czas znaleźć ich wartości:
Uwaga!
Zwroty reakcji można przyjmować dowolnie. Przy
przyjęciu odwrotnego zwrotu do rzeczywistego reakcja wyjdzie ujemna.
Jako pierwszą wyznaczmy poziomą reakcję HA:
HA = 0
Ponieważ w układzie nie ma żadnych reakcji poziomych HA = 0. Czas poszukać reakcji VB. Wyznaczymy jej wartość za pomocą warunku na sumę momentu względem punktu A. Wybraliśmy ten punkt, ponieważ przecina go reakcja VA, której jeszcze nie znamy. Dzięki temu będziemy mieć równanie z jedną niewiadomą.
6VB = -3P - 3Q /:6
VB = 0.5(-P - Q) = 0.5(- 10 - 15)
VB = - 12.5 kN
Teraz czas na obliczenie ostatniej reakcji. Zastosujemy ten sam schemat, lecz tym razem moment policzymy względem punktu B.
VA×6 - P×4.5 + Q×3 + P×1.5 = 0
6VA = 3P - 3Q /:6
VA = 0.5(P - Q) = 0.5(10-15)
VA = - 2.5 kN
Dobrą praktyką jest sprawdzenie otrzymanych wyników. Zrobimy to sumując pionowe siły i sprawdzając czy wynikiem będzie 0.
ΣY = 0?
- VA + P - Q - P + VB = 0
- (- 2.5) + 10 - 15 - 10 - (- 12.5) = 25 - 25 = 0
Warunek został spełniony. Rozwiązanie jest poprawne.
Czas przejść do wykresów. Rozpoczniemy od wykresów momentów gnących. Wykresy można rysować wyprowadzając przepisy funkcyjne, bądź po prostu obliczając wartości w charakterystycznych punktach pamiętając o kilku zasadach. Przedstawimy 2 sposoby równocześnie. Rozpoczniemy w punkcie A. Najpierw wprowadźmy na rysunek obliczone reakcje.
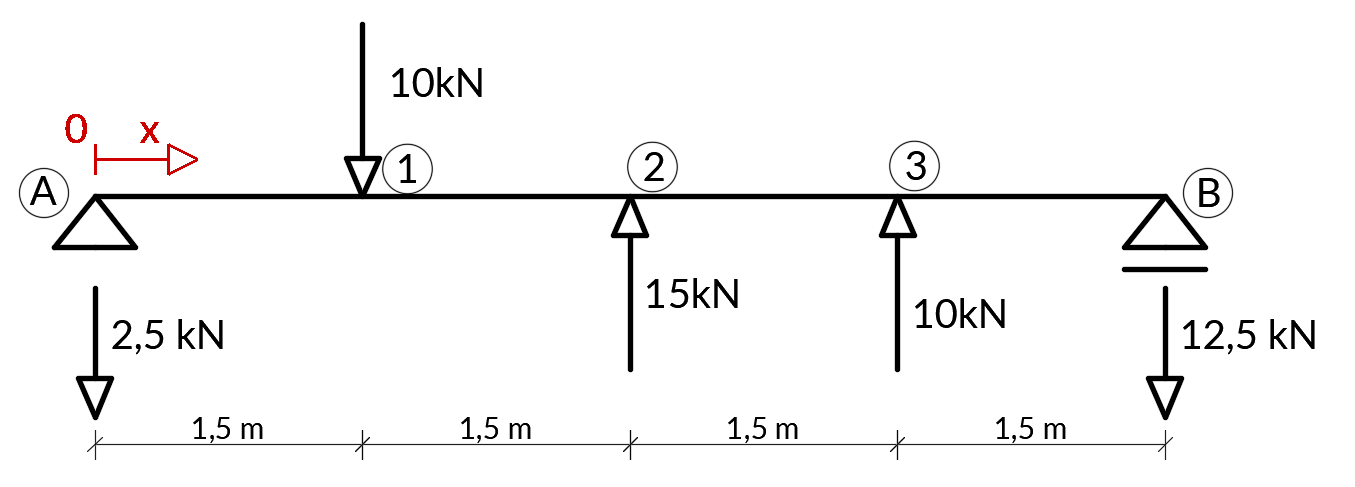
Reakcje wyrysowaliśmy juz zgodnie z ich zwrotami, dlatego pozbyliśmy się minusów. W punkcie A narysowaliśmy początek układu współrzędnych, w którym będziemy opisywać przebieg wykresów sił wewnętrznych (jeżeli rysujemy wykresy bez przepisów funkcyjnych nie trzeba tego robić). Na samym początku wypiszmy to co już wiemy: na końcach belki nie mamy żadnego momentu skupionego, zatem:
Teraz musimy się zastanowić co będzie się działo na odcinku pręta od punktu A do punktu 1. Reakcja w podporze A kręci względem punktu 1 w lewo. Zatem będzie to moment ujemny (jeśli nie wiesz jak się znakuje siły wewnętrzne zajrzyj tutaj w zakładkę "siły wewnętrzne"). Reakcja o wartości 2.5 na ramieniu x daje moment M(x).

M1A(x) = -2.5x
Dla tego przedziału możemy obliczyć teraz 2 skrajne wartości:
M1A(1.5) = -2.5×1.5 = -3.75 kNm
Wiedząc, że ujemne wartości momentu gnącego odkłada się po górnej stronie wykresu możemy przenieść na rysunek to co obliczyliśmy.
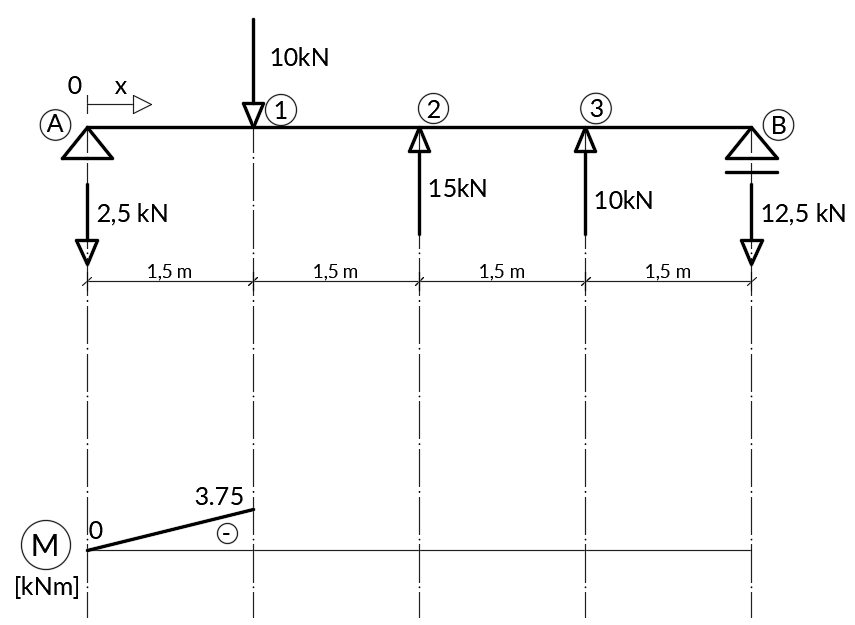
Spróbujmy teraz wyznaczyć funkcję momentu dla przedziału 1-2. Oprócz reakcji z podpory A dochodzi nam siła P = 10kN z punktu 1. Przepis funkcyjny będzie wyglądał następująco:
M21(x) = -2.5x - 10(x-1.5)
M21(1.5) = -2.5×1.5 - 10×(1.5-1.5) = -3.75 kNm
M21(3) = -2.5×3 - 10×(3-1.5) = -22.5 kNm
Pamiętając, że układ współrzędnych zaczyna się w punkcie A rozpoczynamy od uwzględnienia reakcji na podporze. Jej ramię nadal wynosi "x". Ponieważ Siła P jest oddalona od punktu A o 1.5m musimy tą wartość odjąć przy wyliczaniu momentu od tej siły. Potwierdzeniem dobrze napisanej funkcji jest wynik w punkcie x=1.5m, który jest taki sam jak obliczony w poprzednim punkcie. Wykres momentów z wyjątkiem miejsc, gdzie występują momenty gnące musi być zawsze ciągły. Czas umieścic wyniki na wykresie:

Analogicznie postąpimy w następny przedziale 2-3.
M32(x) = -2.5x - 10(x-1.5) + 15(x-3)
M32(3) = -2.5×3 - 10×(3-1.5) + 15×(3-3) = -22.5 kNm
M32(4.5) = -2.5×4.5 - 10×(4.5-1.5) + 15×(4.5-3) = -18.75 kNm
Pamiętając, że na końcu belki musimy mieć MB=0 możemy dokończyć wykres.

Zróbmy jeszcze małe sprawdzenie. Po pierwsze możemy zauważyć, że wszędzie pod siłami widzimy załamania wykresu w kierunku ich działania. To nie jest przypadek, tak jest zawsze, zatem warto sprawdzać czy tak rzeczywiście jest. Zróbmy jeszcze obliczenia sprawdzające dla przedziału B-3, jednak przenieśmy układ współrzędnych do punktu B. Będzie się to prezentować w ten sposób:
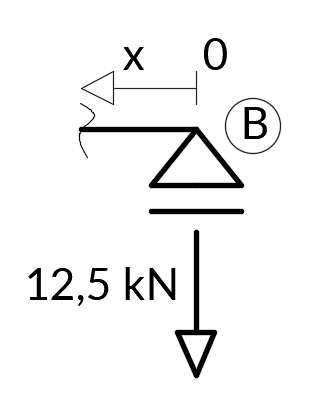
M3B(x) = -12.5x
M3B(1.5) = -12.5×1.5 = -18.75 kNm
Wyznaczyliśmy wartość w punkcie 3 od strony punktu B. Wyszło nam to samo, więc wykres momentów jest poprawny.
Czas zabrać się za wykres sił tnących V. Można to zrobić na kilka sposóbów. Wiadomym jest, że siły tnące są pochodną momentów. Jednak mało kto lubi liczyć pochodne, dlatego tutaj zrobimy to prościej. Na szczęście siły tnące są o wiele łatwiejsze od momentów gnących. Przejdźmy zatem od razu do wyznaczenia funkcji V(x) dla przedziału A - 1.
V1A(x) = -2.5
V1A = -2.5 kN
Jak widzimy w porównaniu do M(x) brakuje w równaniu zmiennej "x". To naturalne ponieważ pochodną z x jest 1. Można wywnioskować, że funkcja V(x) będzie stała. Można ten zapis uprościć i pominąć wypisywanie funkcji:
V1-2 = -2.5 - 10 = -12.5 kN
V2-3 = -2.5 - 10 + 15 = 2.5 kN
V3-B = -2.5 - 10 + 15 + 10 = 12.5 kN
W ten prosty sposób otrzymaliśmy juz wartości dla wszystkich przedziałów. Możemy narysować wykres.

W przeciwieństwie do wykresu momentów tnące ujemne można odkładać po dowolnej stronie. Należy jednak zawsze znakować wykres (+/-). W ten sposób rozwiązane zostało pierwsze zadanie.
Jeżeli coś jest niejasne i jeszcze nie do końca wszystko rozumiesz pamiętaj, że możesz do nas napisać. Nie da rady wszystkich wiadomości przelać na kartkę lub ekran monitora. Jeśli potrzebujesz pomocy przejdź tutaj lub odwiedź naszego facebooka.

Na początek znajdźmy wartości reakcji podporowych. Zsumujmy wektory na kierunku X i przyrównajmy do zera.
HA - 10 = 0
HA = 10 kN
Wyznaczmy wartość VB wykorzystując warunek na sumę momentów względem punktu A.
-8×VB + q×8×4 = 0
Na pierwszy rzut oka widać, że z siłami rozłożonymi postępuje się inaczej niż przy siłach skupionych. To nie do końca prawda. Obciążenie tego typu działa na jakiejś długości, zatem jeżeli przemnożymy wartość obciążenia q przez tą długość otrzymamy zastępczą siłę skupioną Q.

Zastępczą siłę skupioną umieszczamy w środku ciężkości obciążenia rozłożonego. Dla prostokąta w połowie długości. Możemy to wszystko zapisać w następujący sposób:
ΣMA = 0
-8×VB + Q×4 = 0
-8×VB + q×8×4 = 0
-8VB + 32q = 0
8VB = 32q /: 8
VB = 4q = 8 kN
Pozostało znaleźć ostatnią niewiadomą. Zsumujmy wektory na osi Y.
-VA -VB +Q = 0
-VA -VB +8q = 0
VA = -VB +8q
VA = 8q - 4q = 8 kN
Znaleźliśmy wszystkie reakcje. Jeżeli nadal nie rozumiesz skąd to wszystko się wzięło sprawdź naszą ofertę.
Wyprowadźmy przepisy funkcyjne dla momentów gnących.
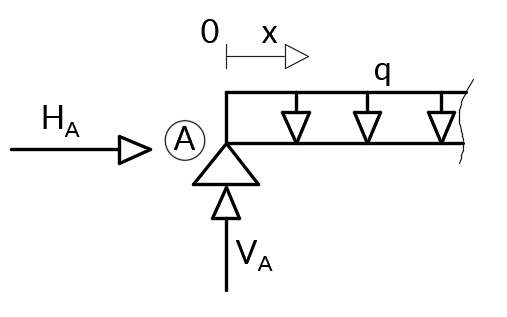
Na początek należy zaznaczyć, że pozioma reakcja HA działa w osi belki, zatem nie bierze udziału w jej zginaniu.
Na długości całej belki obciążenie jest stałe, więc mamy jeden przedział funkcyjny A-B. Spróbujmy rozpisać funkcję.
Zapis się trochę skomplikował w porównaniu z przykładem nr 1.
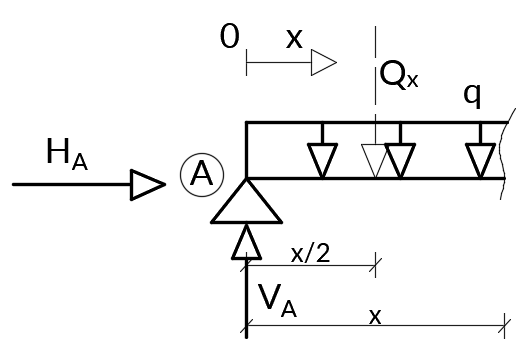
Rozjaśni to powyższy rysunek. Najpierw należy zamienić obciążenie rozłożone q na siłę skupioną Qx. W tym celu tak jak wyżej mnożymy obciążenie q przez długość działania, teraz jest to "x":
Teraz potrzebujemy ramię, na którym działa siła Qx. Jest to połowa długości działania obciążenia, czyli "x/2". Powstaje nam zatem równanie:
M(x) = VA×x - q×x×x/2
M(x) = VA×x - q×x2/2
M(x) = - qx2/2 + VAx
Zmienna "x" jest w kwadracie - jest to funkcja kwadratowa. Oznacza to, że wykres momentow gnących w przypadku obciążenia rozłożonego (prostokątnego) będzie parabolą. Aby narysować parabolę potrzebujemy minimum 3 punktów. Wyznaczmy wartości na podporach i w środku rozpiętości belki.
W środku - ponieważ w naszym wypadku tam będzie maksimum funkcji momentu. Można to sprawdzić licząc pochodną funkcji M(x), przyrównać ją do zera i wyznaczyć wartość "x". Na tym etapie jednak wystarczy uwierzyć na słowo.
MB = M(8) = -82/2q + 8VA
MB = M(8) = -82/2×2 + 8×8 = -64 + 64 = 0 kNm
M1 = M(4) = -42/2q + 4VA
M1 = M(4) = -42/2×2 + 4×8 = 16 kNm
W obu podporach wyszło nam 0, więc możemy sądzić, że wynik jest poprawny. Narysujmy rozwiązanie:

Jeżeli na tym etapie masz jakieś wątpliwości napisz do nas na facebooku.
Czas na wykres sił tnących. Tutaj też będzie trochę trudniej niż poprzednio.

Napiszmy funkcję dla V(x):
V(x) = VA - q×x
V(x) = 8 - 2x = -2x + 8
Otrzymaliśmy funkcję liniową. Policzmy wartości w tych samych punktach co poprzednio.
VB = V(8) = 8 - 2×8 = -16 kN
V1 = V(4) = 8 - 2×4 = 0 kN
Zilustrujmy otrzymane wyniki.
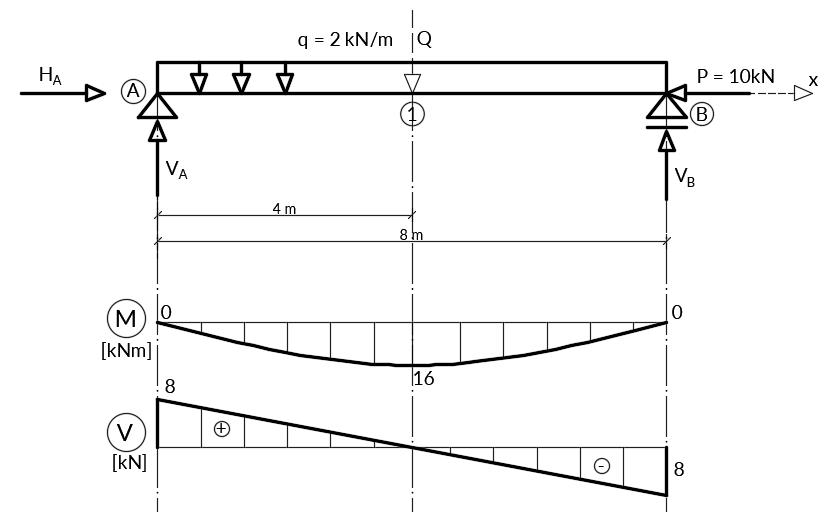
Teraz siły osiowe. Działa tylko jedna stała siła pozioma, więc:
Ujemna, ponieważ jest to siła ściskająca belkę.

Jeżeli coś jest niejasne i jeszcze nie do końca wszystko rozumiesz pamiętaj, że możesz do nas napisać. Nie da rady wszystkich wiadomości przelać na kartkę lub ekran monitora. Jeśli potrzebujesz pomocy przejdź tutaj lub odwiedź naszego facebooka.

Wyznaczenie reakcji:
HC = 0
ΣY = 0
VB = q(1.7 + 2.2)
VB = 7.8 kN
ΣMC = 0
5×VB-q×(1.7 + 2.2)& #215;(1.5 + (1.7 + 2.2)/2) + M - MC = 0
MC = 7.8×5 - 2×3.9×4.7 + 25
MC = 26.95 kNm
Czas wyznaczyć wykresy sił wewnętrznych. Rozpoczynamy w punkcie C i rysujemy w prawą stronę:
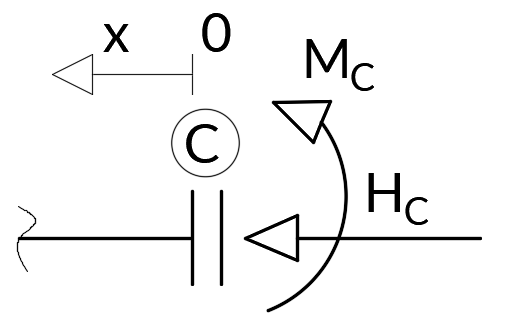
MC-2(x) = 26.95 kNm
Jeżeli w przedziale występuje tylko moment gnący to wykres jest stały.
Dla przedziału 2 - 1:
M2-1(x) = 26.95 - 25 = 1.95 kNm

Przejdźmy na stronę lewą i rozpiszmy przedział A-B
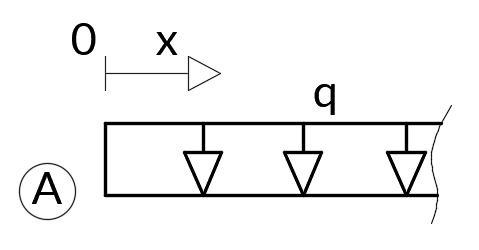
MA-B(x) = -q×x×x/2 = -qx2/2
MA-B(0) = 0 kNm
MA-B(1.7) = -2.89 kNm
MA-B(0.85) = -0.72 kNm
Pozostał przedział B-1
MA-B(x) = -qx2/2 +VB×(x - 1.7)
MA-B(1.7) = -2.89 kNm
MA-B(3.9) = 1.95 kNm
MA-B(2.8) = 0.74 kNm
Graniczne wartości pomiędzy przedziałami wyszły takie same, pozwala to stwierdzić, że rozwiązanie jest poprawne. Jeżeli masz problemy ze zrozumieniem dotychczasowego materiału przejdź tutaj.

Czas na siły tnące. Tym razem bez przepisów funkcyjnych, jeśli chcesz wyprowadź je sam. Najważniejsza jest praktyka.
VBA = -1.7q = -3.4 kN
VB1 = -3.4 + 7.8 = 4.4 kN
V1B = 4.4 - 2.2q = 0 kN
Ponieważ w dalszej części belki nie ma już żadnych sił pionowych wykres sił tnących będzie zerowy.

Jeżeli coś jest niejasne i jeszcze nie do końca wszystko rozumiesz pamiętaj, że możesz do nas napisać. Nie da rady wszystkich wiadomości przelać na kartkę lub ekran monitora. Jeśli potrzebujesz pomocy przejdź tutaj lub odwiedź naszego facebooka.

Zanim przejdziemy do wyznaczenia reakcji trzeba zatrzymać się nad obciążeniem rozłożonym po trójkącie. Pamiętając, że zastepcza wypadkowa Q to pole figury obciążenia i umieszczamy ją w środku ciężkości tej figury, w przypadku trójkąta środek ciężkości znajduje się w 1/3 długości od maksimum obciążenia o wartości q. W przypadku wyznaczenia wartości wypadkowej Q stosuje się wzór na pole trójkąta.

Wyznaczenie reakcji:
HB = 0
ΣY = 0
VB = 1/2ql - 10
VB = 1/2×8.8×6.6 - 10 = 19.04 kN
ΣMB = 0
MB = 10l - 1/2ql×1/3l
MB = 10×6.6 - 1/2×8.8×6.6×1/3×6.6
MB = 2.11 kNm
Przejdźmy do wykresów. Obciążenie po trójkącie to kolejny stopień trudności w przepisach funkcyjnych. Oprócz zmiennej "x" zmienia się również wartość obciążenia.

Aby móc narysować wykres funkcji sił wewnętrznych musimy wyznaczyć funkcję q(x) wykorzystując twierdzenie Talesa:
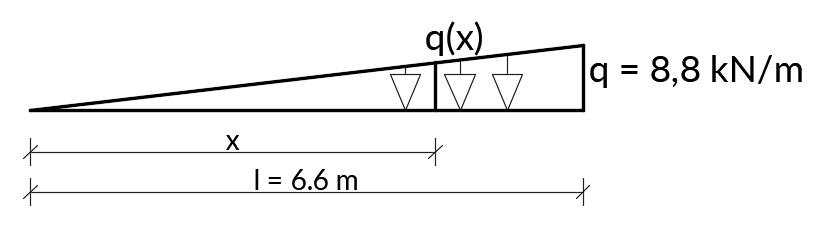
q(x) = qx/l
Czas rozpisać funkcję M(x) dla całej belki (w tym przykładzie jest jeden przedział funkcyjny).
M(x) = Px - 1/2×q/l×x×x×x/3
M(x) = Px - 1/6×q/l×x3
M(x) = -1/6×q/l×x3 + Px
M(x) = -1/6×8.8/6.6×x3 + 10x
M(x) = -0.22x3 + 10x
Jak widać otrzymaliśmy funkcję 3. stopnia. Jak ją narysować? Trzeba znaleźć jej charakterystyczne punkty. Są to miejsca zerowe, maksimum i minimum funkcji. Oprócz tego warto wyznaczyć dodatkowe punkty, które pomogą ją narysować. Aby znaleźć maksimum (minimum) funkcji musimy:
1) Wyznaczyć jej pochodną,
2) Przyrównać do zera,
3) Wyznaczyć niewiadomą "x",
4) Obliczyć wartość maksymalną podstawiając wyznaczone "x" do funkcji M(x).
M'(x) = -0.66x2 + 10
-0.66x2 + 10 = 0
-x2 = -10/0.66
x2 = 15
x = √15 ∨ x = -√15
x = 3.87 m ∨ x = -3.87 m < 0
Jak wiadomo równanie kwadratowe ma dwa rozwiązania, ale odrzucamy ujemne, ponieważ ujemna odległość to twór bez sensu.
Aby znaleźć miejsca zerowe musimy przyrównać do zera M(x) i wyznaczyć niewiadome "x".
-0.22x3 + 10x = 0
x(-0.22x2 + 10) = 0
x1 = 0 ∨ -0.22x2 + 10 = 0
-x2 = -10/0.22
x2 = 45
x = √45 ∨ x = -√45
x2 = 6.71 m > 6.6 m ∨ x3 = -6.71 m < 0
Wykres na długości belki będzie miał tylko jedno miejsce zerowe - w punkcie zero. Pozostałe niewiadome znajdują się poza belką. Aby poprawnie wyrysować wykres wyznaczmy pomocnicze wartości funkcji M(x):
M(0.5l = 3.30) = -0.22×3.303 + 10×3.30 = 25.01 kNm
M(0.75l = 4.95) = -0.22×4.953 + 10×4.95 = 22.55 kNm
M(l = 6.60) = -0.22×6.603 + 10×6.60 = 2.11 kNm
Przy okazji sprawdziliśmy poprawność funkcji, przy wartości równej l = 6.60 m otrzymaliśmy wynik równy reakcji w podporze B. Wykres momentów gnących prezentuje się następująco:
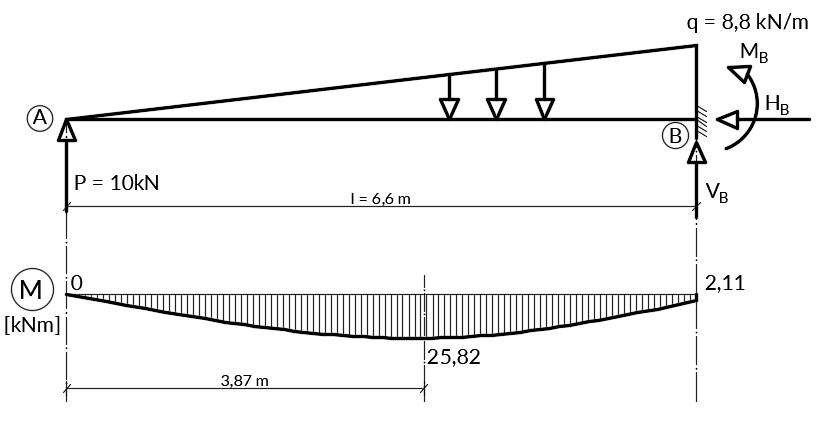
Funkcja sił tnących:

V(x) = P - 1/2×q(x)×x
V(x) = P - 1/2×q/l×x×x
V(x) = P - 1/2×q/l×x2
V(x) = -1/2×8.8/6.6×x2 + 10
V(x) = -0.67×x2 + 10
Tutaj należy zauważyć, że V(x) powinno być równe M'(x), u nas różni się o 0.01 z powodu zaokrągleń. Miejsce zerowe tej funkcji już mamy - obliczyliśmy je przy okazji wyznaczania wartośći maksymalnej M(x). Ponieważ V(x) jest funkcją kwadratową i nie znamy jej przebiegu musimy wyznaczyć jej minimum i maksimum, aby poprawnie ją wyrysować.
V'(x) = -1.33x
V'(x) = 0
x = 0
Wierzchołek funkcji V(x) będzie w punkcie x = 0. Czas wyrysować funkcję V(x) pamiętając, że jest to funkcja kwadratowa:
V(6.6) = -0.67×6.62 + 10 = -19.04 kN
Wartość w punkcie x = 6.6 m zgadza się z obliczoną przez nas reakcją VB.

Jeżeli coś jest niejasne i jeszcze nie do końca wszystko rozumiesz pamiętaj, że możesz do nas napisać. Nie da rady wszystkich wiadomości przelać na kartkę lub ekran monitora. Jeśli potrzebujesz pomocy przejdź tutaj lub odwiedź naszego facebooka.

